四角すい 四角錐 体積計算 公式 求め方 高さ 底面積 自動 長方錐 方錐 volume四角錐台の体積の求め方 中学一年の者です。とても急いでいるので質問が乱暴になってしまってすいません。 どなたか、四角錐台(四角錐の上部を切り取ったようなもの)の体積の求め方を教えてください!! お願いします。9 超緊急です!!四角錐台の体積の求め方 10 上辺25、下辺355、高さ54の、四角錐体の体積の求め方を、数学が苦手な自分でも分かるように説明 関連するカテゴリからQ&Aを探す

トップ100 四角錐体積公式 ただぬりえ
四角錐台体積 公式
四角錐台体積 公式-(四)角錐台は(四)角錐を底面に平行な平面で切った立体でなければなりません。 別な言い方をすると,上底面と下底面が相似な四角形,AB=ab でなければなりません。 元になる角錐は,頂点が底面の重心などの真上にある必要はありません。四角錐を平面で切った立体の体積比は (向かい合う1組の辺比の積) x (もう1組の辺比の平均) になるようです でも、これは底面が平行四辺形以上の特殊な場合でないと使えないし、そもそも四角錐を縦に切る作業がわかってしまえば面倒でもないので意味なし


1 1 負數與數線
四角錐の体積=底面積×高さ× より 四角錐の高さ=四角錐の体積÷底面積×3で求めることが出来ます。 ここで、底面積=12×12=144(cm²)であることから 求める四角錐の高さ=432÷144×3=9(cm)となります。 答え 9cm ~立体の体積・表面積を求める公式ある図形の体積 切断面の高さ ・・・ などが話題となり、まとめられてきた。このページでは、立体図形の体積について、さらなる 考察を試みたいと思う。 例題 上面、下面が平行(各面の長方形の辺どうしが平行)な四角錐台の体積を求めよ。問題 右の図の正四角錐の体積と表面積を求めよ。 解 体積 1 3 ×102× 12=400 (cm3) 表面積底面積は 100 cm2。側面は合同な二等辺三角形だから, 1 2 ×10×13 ×4+100=360 (cm2) 答 体積 400 cm3,表面積 360 cm2 139 次の図の正四角錐の表面積を求めよ。
これが四角錐の高さになる。 AMはACの 1 2 なので AM=6 2 ≫ O A C 15cm 15cm M 12 2 cm 6 2 cm OAMで三平方の定理を使うと 15 2 =OM 2 (6 2) 2 OM 2 = OM 2 =153 OM=±3 17 OM>0よりOM=3 17 よって、高さ3 17, 底面積12×12=144 体積 144×3 17 ÷3=144 17 cm 3 ≫類題練習正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 なぜ\(\dfrac{1}{3}\)をかけるのかは、きちんと説明するには高校生で習う"積分"という分野の知識が必要になるので、今回は省略します。V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体
正四角錐台の体積 のことなんじゃないかな。 プリンみたいな立体だよ。 正四角錐台は台形の立体バージョンにみえるし、たぶんそう。。 そこで今日は台形の体積のかわりに、 正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて。四角錐の体積=底面積×高さ× より 四角錐の高さ=四角錐の体積÷底面積×3で求めることが出来ます。 ここで、底面積=12×12=144(cm²)であることから 求める四角錐の高さ=432÷144×3=9(cm)となります。 答え 9cm ~立体の体積・表面積を求める公式V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体



同加為精密工業的全方位供應平台 同加貿易不但保持價格的競爭力 也致力於資源的整合與問題解決能力的提升 包含對上以敬 對下以慈 對人以和 對事以真的落實與延伸 官網的設立 希望能站在客戶的面向 提供最完整的資訊 最低的採購成本 最簡單的需求尋找 最佳的



基礎 角錐的點 邊 面 Youtube
四角錐台の体積の求め方 中学一年の者です。とても急いでいるので質問が乱暴になってしまってすいません。 どなたか、四角錐台(四角錐の上部を切り取ったようなもの)の体積の求め方を教えてください!! お願いします。角錐 P12 角錐台 P12 楔形 P12 直円柱 P12 斜円柱 P12 直円錐 P12 平均自乗誤差 P13 円板の最大応力(σmax)と最大たわみ(ωmax) P96 長柱の座屈 P97 各種断面形の軸のねじり P97 体積(V) 重心Gの位置(z)四角錐の体積を求めるときに気をつけたいのは、 必ず\(\frac{1}{3}\)を掛ける ことです。 四角錐、円錐など、てっぺんがとんがっている錐体と呼ばれる立体の体積は必ず\(\frac{1}{3}\)を掛けてください。 よって、計算は次のようになります。



壮大 台形 体積 求め 方 壁紙 配布


博客來 藝數摺學 18堂從2d到3d的 摺紙數學課 讓幾何從抽象變具體 發現數學的實用 趣味與美 對應108十二年國教新課綱
ある図形の体積 切断面の高さ ・・・ などが話題となり、まとめられてきた。このページでは、立体図形の体積について、さらなる 考察を試みたいと思う。 例題 上面、下面が平行(各面の長方形の辺どうしが平行)な四角錐台の体積を求めよ。体積の利用 \(ce\) の長さは、底面を三角形 \(oab\) と見たときの 三角錐の髙さになっています。 つまり「体積」から計算できます。 その1で、「(1)この正三角錐の体積を求めなさい。」 を解説しております。 体積は \(6cm^3\) です。 底面が \(oab\) 高さを \(ce\)角錐 P12 角錐台 P12 楔形 P12 直円柱 P12 斜円柱 P12 直円錐 P12 平均自乗誤差 P13 円板の最大応力(σmax)と最大たわみ(ωmax) P96 長柱の座屈 P97 各種断面形の軸のねじり P97 体積(V) 重心Gの位置(z)


劉徽與出入相補原理


四角錐 Square Pyramid Japaneseclass Jp
四角錐台の体積の求め方 中学一年の者です。とても急いでいるので質問が乱暴になってしまってすいません。 どなたか、四角錐台(四角錐の上部を切り取ったようなもの)の体積の求め方を教えてください!! お願いします。四角錐を平面で切った立体の体積比は (向かい合う1組の辺比の積) x (もう1組の辺比の平均) になるようです でも、これは底面が平行四辺形以上の特殊な場合でないと使えないし、そもそも四角錐を縦に切る作業がわかってしまえば面倒でもないので意味なし9 超緊急です!!四角錐台の体積の求め方 10 上辺25、下辺355、高さ54の、四角錐体の体積の求め方を、数学が苦手な自分でも分かるように説明 関連するカテゴリからQ&Aを探す



面積 体積 計算ツール 福井鋲螺株式会社 冷間鍛造 冷間圧造 ヘッダー加工の専門メーカー リベット 特殊形状パーツおよび省力機器の製造 販売



雙錐台 在幾何學中 雙錐台又稱雙平截頭體 英語 Bifrustum 是指 百科知識中文網
正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱の体積 楕円柱の体積 直円錐の体積 斜切円錐の体積 一部が欠けた直



柱體和錐體 23 直圓錐的表面積計算 Youtube


几何学 Wikiwand


劉徽與出入相補原理


瑞光儀器有限公司


四角錐台の体積v H 6 Ab Ab 2 Ab Ab の公 Yahoo 知恵袋



公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成



Woa1 B型鉄シリケート組成物及び窒素酸化物還元方法 Google Patents



土方放坡係數計算公式 每日頭條


美しい正四角錐体積公式 壁紙配布



50 グレア 四角錐面積 壁紙配布


1 1 負數與數線


四角錐台の体積の公式について この画像のように上下面が共に長方形 Yahoo 知恵袋



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ
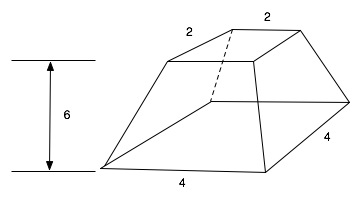


モスクワ数学パピルス Wikipedia
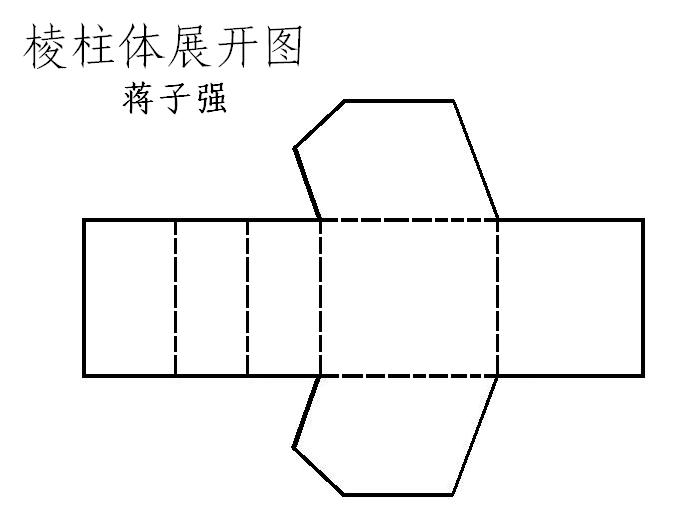


稜柱 含義 介紹 對角線的求法 性質 直稜柱 展開圖 側面積 體積 分類 表示 中文百科全書



台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ


劉徽與出入相補原理


哥白尼的實驗室 數學教具 5cm十七形幾何容器 藍蓋 Usl遊思樂 幾何形體角柱角錐體積概念 蝦皮購物



錐台 維基百科 自由的百科全書



Phatlabaudio Taiwan 首页 Facebook


藝數摺學 18堂從2d到3d的 摺紙數學課 讓幾何從抽象變具體 發現數學的實用 趣味與美 對應108十二年國教新課綱 三民網路書店



錐體體積 1 3柱體體積的3種證明法 Ishewh的創作 巴哈姆特



体積測定によって検証する土塁の取崩しと土橋の造成



70以上三角錐体積公式 壁紙引用画像hd


几何学一 图文 百度文库


几何学一 图文 百度文库



Junior High数学的 体積 表面積 側面積の公式 筆記 Clear
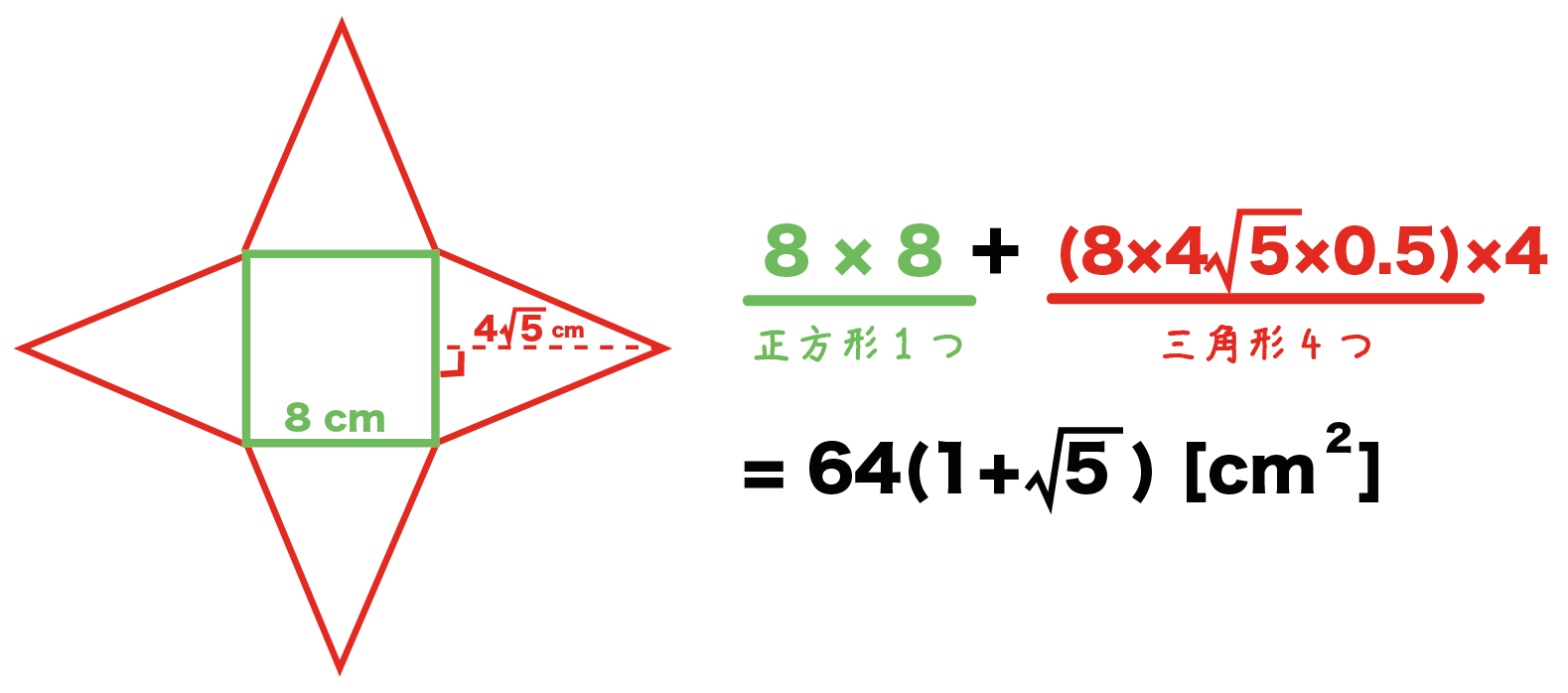


壁紙押入れ 最も人気のある 正四角錐体積公式



公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成



五面體 维基百科 自由的百科全书



稜錐 維基百科 自由的百科全書



台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ
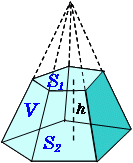


角錐台の体積 高精度計算サイト



公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成



錐台 Wikiwand


四角錐台の展開図の書き方が知りたいです 計算じゃなくて四角錐台の Yahoo 知恵袋



三角錐柱 维基百科 自由的百科全书


Bottom



有效運用基本能力評估 網上學與教支援 動態幾何軟件 Dynamic Geometry Software 於立體圖形學與教上的應用 Ppt Download



四角錐台の高さを求めたいです 画像のような四角錐台の高さを求めたい 数学 教えて Goo


1 1 負數與數線



Woa1 B型鉄シリケート組成物及び窒素酸化物還元方法 Google Patents



公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成


立体図形の体積


角錐台 Japaneseclass Jp



四角錐の展開図の切り出し 名古屋市立大学14年 理系のための備忘録



六角錐 在几何形状 六角形金字塔是指底表面的六角锥体 从六边



台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ



四面體 維基百科 自由的百科全書
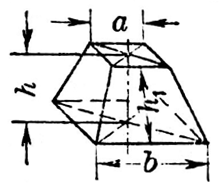


正方角锥台体积计算器 计算专家



锥台 Wikiwand
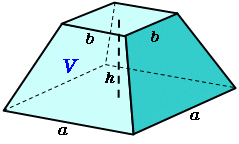


トップ100 角錐台体積



四角錐 分類 詹森多面體 相關多面體 中文百科全書
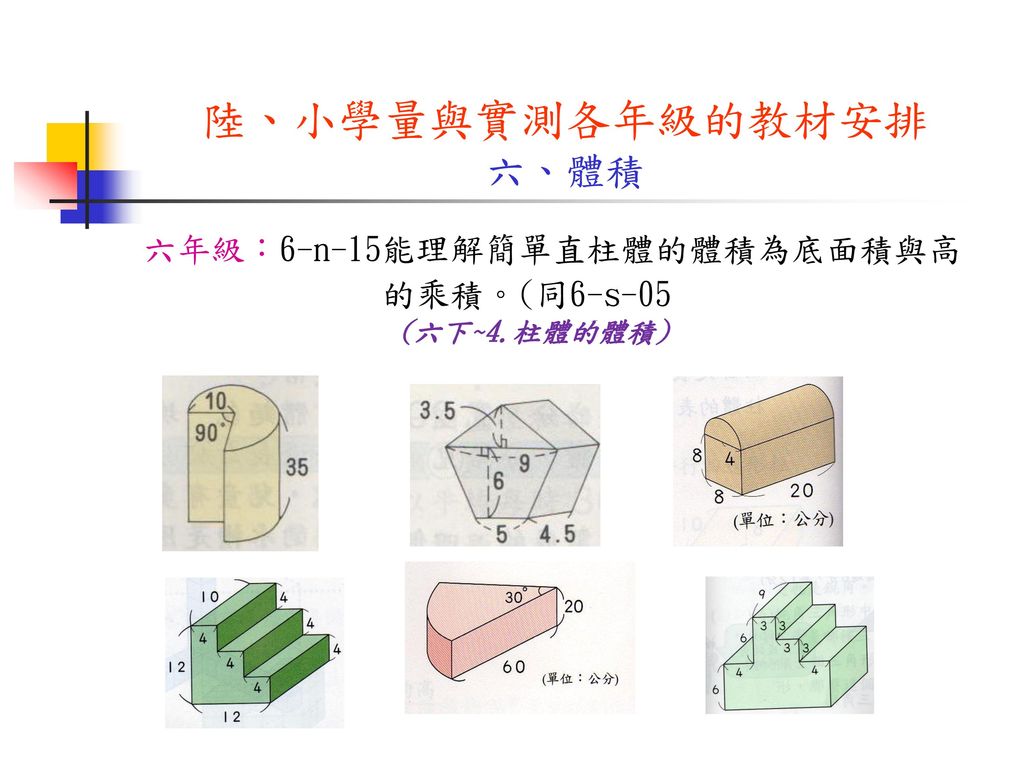


從數學基本學力檢測探討數學量與實測的教學策略 Ppt Download
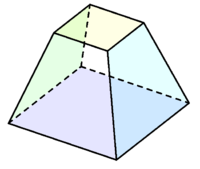


六面體 Wikiwand
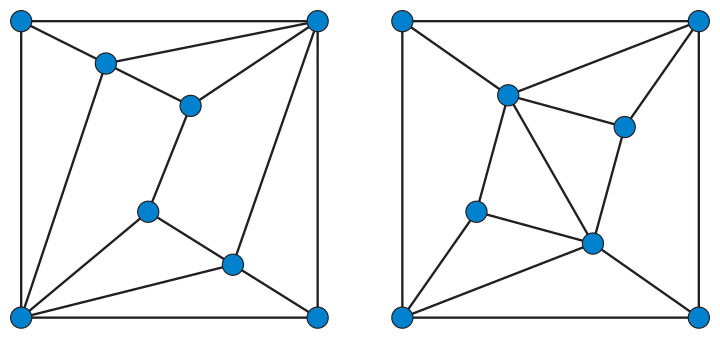


九面體 Wikiwand



四方锥台体积公式锥台的体积公式是什么



正四面积体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com



トップ100 四角錐体積公式 ただぬりえ



公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成



几何学 维基百科 自由的百科全书


逆定理 Www Dingjisc Com



Woa1 B型鉄シリケート組成物及び窒素酸化物還元方法 Google Patents


内角公式 多边形内角公式 多边形内角和 多边形的内角



高二空間問題四角錐求高四腳錐求體積金字塔求體積求側面與底面的兩面角餘弦空間問題高二下第一章106龍騰課後卷計算題


四角錐台の公式 体積 側面積 表面積 数学 エクセルマニア


正四角錐台の体積の求め方 Media Qikeru Yahoo 知恵袋


劉徽與出入相補原理



四角錐台の体積 高精度計算サイト



4つの高さが違う体積の計算 底面の形0 5cm 7 5cmの長方形高さが7cm 3 数学 教えて Goo


四角錐台 台形の立体ver の体積の求め方なんですが 下面積 上面積 Yahoo 知恵袋



Keisan



70以上三角柱体積公式 壁紙引用画像hd



円錐台 体積公式


