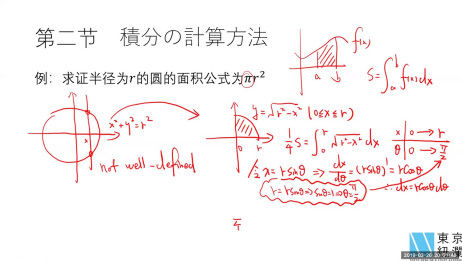
球の表面積の公式 中2男子です。 なぜ球の表面積の公式は 4πr^2 で求めることができるのですか。 自分は中1の3学期の時に球の表面積について習いました。 その時先生は「みなさんにはなぜ表面積の公式(円の面積) = π r 2 という公式が作られる。 円の面積公式の、厳密な意味での証明は、三角関数の微分積分を待たなければならな い。しかし、この証明に出会える日本の高校生は、現行のカリキュラムでは非常に少ない。今回は、球の体積・表面積の求め方(公式)について書いていきたいと思います。 球の体積の求め方公式 球の表面積の求め方公式 球の体積・球の表面積を求める問題 問題① 《球の体積の求め方》 《球の表面積の求め方》 問題② 《球の体積の求め方》 《球の表面積の求め方》 問題
球的体积和表面积 西伯利亚 Ppt Download
球体 面積 体積 公式
球体 面積 体積 公式-3) 円柱面x2 y2 = a2 の円柱面x2 z2 = a2 の内部にある部分の曲面積を 求めよ。 4) xy 平面上のC1 級曲線y = f(x) (a • x • b) をx 軸のまわりに1回転 してできる曲面の曲面積は S = 2 Z b a jf(x)j p 1(f0(x))2dxとなることを証明せよ。 5) 曲面z = Arctan(y=x) (x;y > 0) の円柱面x2 y2 = a2 の内部にある部 分の曲面積を前述の通り、球体の表面積 v を求める公式は、次の通りです。 \begin{align*} V = 4 \pi r^2 \end{align*} この式に出てくる文字の意味は、次の通りです。



球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく
回転体の表面積も求めよう! では次,曲線をx 軸やy 軸のまわりに回転してできる回転体の曲面の表 面積を求める公式についても解説しておこう。 (Ⅰ) について,微小区間x, +Δ における 微小な曲面の表面積 ΔS は,図12 より覚えなくていい「円の面積」 算数は得意なのに数学が苦手なひとのためのブログで、 円の面積円周半径覚えなくていい「球の表面積・体積」 算数は得意なのに数学が苦手なひとのためのブログで、 球の表面積円周極間の距離 ってことをやった。どちらも底辺高さ定数の形だね。①球の体積の公式の求め方 球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を 考察しておこう。下の図1において、球の中心から距離 x の点で切った断面である円の半径は √(r 2 -x 2) であるから、円の面積は、S(x)=π(r
円の面積を求める公式は、S = πr^2 で表されます。このページでは、円の面積の求め方を、計算問題と共に説明しています。また、公式の導き方のイメージも説明しています。この公式の最初の発見者アルキメデスは 、外接円筒の側面への射影が面積を保つという事実から公式を導いた 。 公式を導く別なやり方は、これが同じく半径 r の球の体積の r に関する 微分 に等しいという事実を利用することである。円の面積を求める公式は、S = πr^2 で表されます。このページでは、円の面積の求め方を、計算問題と共に説明しています。また、公式の導き方のイメージも説明しています。
実際に曲面積の公式を導出してみましょう。 上の図のような平行四辺形を考えるためにベクトル , を考えます。 すると、平行四辺形の面積は と の外積の長さで求めることができますね。 ベクトル , の外積を求めると*1、\\begin{align*}複雑な公式であっても、その場で思い出すことができますね! 私は今でも語呂合わせで思い出すことがありますw あ! 語呂合わせで公式は覚えたけど どっちが体積で、どっちが表面積だっけ? というようにごちゃごちゃになっちゃう人も多いです。実際に曲面積の公式を導出してみましょう。 上の図のような平行四辺形を考えるためにベクトル , を考えます。 すると、平行四辺形の面積は と の外積の長さで求めることができますね。 ベクトル , の外積を求めると*1、\\begin{align*}


微积分下的不规则图形的体积计算原理 科学探索



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
線形代数 行列式(2次, 3次) サラスの公式 253k件のビュー √ 平方根の微分 158k件のビュー 第三者不正中継チェックサイトメモ 21 145k件のビュー球の体積と表面積 半径 \(r\) の球の体積と表面積を求める公式は以下のようになります。 \(球の体積=\displaystyle \frac{4}{3}\pi r^3\) \(球の表面積=4\pi r^2\) 「なぜこの公式が成立するのか」については中学生の知識の範囲外です。今回は、球の体積・表面積の求め方(公式)について書いていきたいと思います。 球の体積の求め方公式 球の表面積の求め方公式 球の体積・球の表面積を求める問題 問題① 《球の体積の求め方》 《球の表面積の求め方》 問題② 《球の体積の求め方》 《球の表面積の求め方》 問題


球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社



球的面积公式 第1页 一起扣扣网
球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半回転体の表面積も求めよう! では次,曲線をx 軸やy 軸のまわりに回転してできる回転体の曲面の表 面積を求める公式についても解説しておこう。 (Ⅰ) について,微小区間x, +Δ における 微小な曲面の表面積 ΔS は,図12 より球の体積基準比表面積(単位体積当たりの表面積) \(\displaystyle \frac {6}{D}\) いちいち半径の公式から換算するのは能率が悪い。 円と球の公式


扇形面积面积公式 体积 表面积计算公式大全 尚书坊


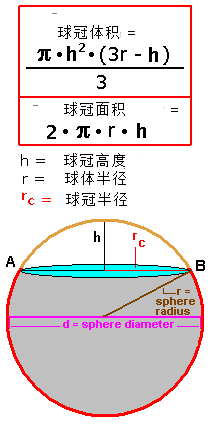
球冠 维基百科 自由的百科全书
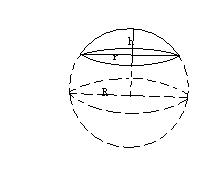
球欠 (spherical segment):球を一つの平面で切った立体 球冠 (球帽,spherical cap):球欠の側面部分 球台 (spherical segment):球を二つの平行な平面で切った立体 球帯 (spherical zone):球台の側面部分 球欠と球台は立体,球冠と球帯は曲面です。球欠は球の一部が欠けたもので,球帽は帽子表面積は3通りの方法を解説します。 積分の感覚をつかむよい練習になります。 球の体積と表面積の公式について まずは証明の前に,球の表面積と体積に関して認識しておくべきことを整理しておきました。 以下の語呂合わせで覚える方法が有名です:★ 数学公式集 図形・面積・体積 For example 扇・弓・円・楕円・円錐・三角錐・角錐・球体・楕円体・台形・三角形・ など ・・


不完整球体表面积求不规则半球体的表面积


体积公式计算圆台体积公式是什么 如何计算圆台的体积
(円の面積) = π r 2 という公式が作られる。 円の面積公式の、厳密な意味での証明は、三角関数の微分積分を待たなければならな い。しかし、この証明に出会える日本の高校生は、現行のカリキュラムでは非常に少ない。表面積の公式 「心配アール2乗」と覚える。 問題 (1) 半径 1cm の球の体積と表面積は求めなさい。 (2) 半径 2cm の球の体積と表面積は求めなさい。 (3) 半径 3cm の球の体積と表面積は求めなさい。 (4) 半径 4cm の球の体積と表面積は求めなさい。球の表面積の公式 中2男子です。 なぜ球の表面積の公式は 4πr^2 で求めることができるのですか。 自分は中1の3学期の時に球の表面積について習いました。 その時先生は「みなさんにはなぜ表面積の公式



球の表面積と体積の公式 数学fun


数学趣谈 球面积公式的不同导出方法 参考网
どう?球の表面積をおぼえるなんて簡単でしょ??笑 まとめ:球の表面積の求め方の公式は「ヒョウ」で覚える 球の表面積の公式はおぼえられた?? 9匹(球)のヒョウ(表面積)の捕獲に失敗(4π)したあるじ(rの二乗) という語呂さえおぼえておけ表面積の公式 「心配アール2乗」と覚える。 問題 (1) 半径 1cm の球の体積と表面積は求めなさい。 (2) 半径 2cm の球の体積と表面積は求めなさい。 (3) 半径 3cm の球の体積と表面積は求めなさい。 (4) 半径 4cm の球の体積と表面積は求めなさい。①球の体積の公式の求め方 球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を 考察しておこう。下の図1において、球の中心から距離 x の点で切った断面である円の半径は √(r 2 -x 2) であるから、円の面積は、S(x)=π(r



球表面积公式 第1页 一起扣扣网
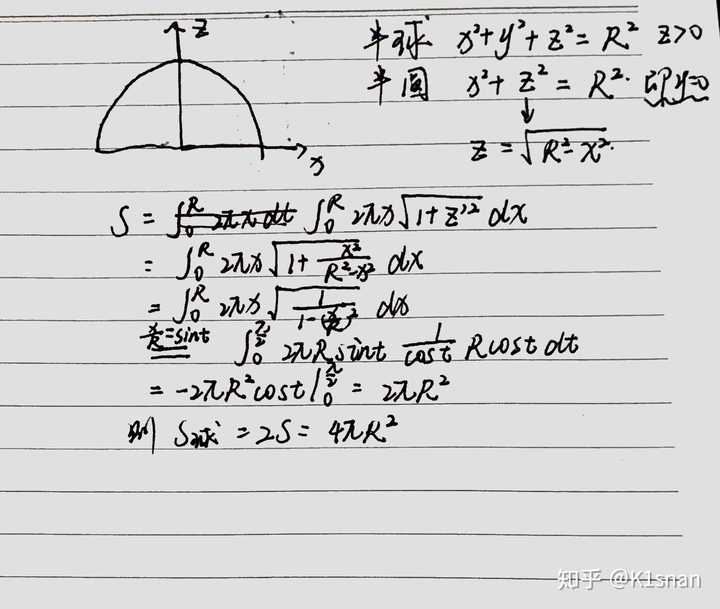


为何对圆周长公式积分无法得到球表面积公式 知乎
数学では「公式を丸暗記」というのはタブーに近いですが、今回はある意味しかたありません。 まずはこの公式をしっかりと覚えましょう! 公式の覚え方 それでは球体積公式を確実に覚えるためのコツを2つ紹介します。



计算体积 面积公式大全下载 Word模板 爱问共享资料



中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく


球体积的前世今生 科普中国


数学趣谈 球面积公式的不同导出方法 参考网


在球的体积公式中 为什么会出现三分之四这个奇怪的系数 体积 公式 系数 新浪新闻



求两个球的体积并 Starlet Kiss的博客 Csdn博客


脑洞大开的微积分



球缺体积和球冠表面积的计算公式及应用 晨起尘又落 Csdn博客


常用体积计算公式 电子工程世界 Eeworld


写给5年级的学生 球公式是如何推导出来的 表面积


圆形周长 面积 体积及椭圆周长 面积计算公式 徐州峰华网架加工电话 加油站罩棚 加气站罩棚网架 球形网架加工安装厂家


对球体表面积的证明有什么问题 结果是p 178 R 178 设球半径为r 表面积为s S就相当于对球 上圆的周长一般式积分 S 2 0 R 2p根号下 R 178 X 178 Dx 4p 0 R 根号下 R 178 X 178 P 作业 慧海网



求球体的表面积和体积 修也 Csdn博客 球体表面积



球的体积和表面积 西伯利亚 Ppt Download



球扇形 球心角体 体积 表面积计算公式与在线计算器 三贝计算网 23bei Com



球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく


体积公式面积公式 作业 慧海网


圆球表面积 球体表面积的公式证明 篆体字转换器



數學真魅 球體體積公式derivation Of Formula Of Volume Of Sphere



球体表面积 第1页 图说健康



数学史话之尤里卡阿基米德阿基米德是一个物理学家和数学家 上网瞧瞧



常用球缺的面积 体积 重心高度 斜边长度计算 细点设计



球體表面積及體積的推導 每日頭條


面积公式 360百科



すごい球体面積公式 壁紙配布


如何用微积分证明圆球表面积计算公式 相关视频 用微积分证明圆的面积公式 爱言情



球体面积公式推导图解 第1页 图说健康



球的体积公式和表面积公式 公式大全 就上高考网



球の体積と表面積 公式と計算問題と証明 Irohabook



圆锥与球与圆柱


圆面积与球体积的统一探讨 参考网


球体表面积公式球体表面积球体表面积 公式证明 爱华网



球的體積求導便是球的表面積 互為逆運算 降維與升維 每日頭條


球体公式球体表面积公式



图解球体表面积和体积正确计算方法及计算公式 天涯杂谈 论坛 天涯社区



球の体積公式の微分が表面積になっている理由 Youtube



球体面积公式是什么 球的面积公式是什么 球体的体积公式是什么 球体积公式是什么


学军小筑 各种图形计算公式 给孩子留着


面積公式 常見面積定理 圓公式 扇形公式 圓環面積 三角形公式 海倫公式 坐標公式 中文百科全書



面積及體積 Dse Maths Helper



部分球面积 球面积的计算公式 球的表面积计算公式 球体积公式



圆球体面积计算公式 你搜我答


物理方法解决数学问题 二 Archimedes与球体积公式 Matrix67 The Aha Moments



面积 维基百科 自由的百科全书


Wqco2oz5knmt M


祖沖之 球體公式及其他 註釋


球的体积公式 球的体积公式画法


球面积计算公式 体积公式 球面积计算 球的面积公式


多变量微积分笔记 球坐标系 我是8位的 博客园


球冠在线计算器 在线计算 在线计算器 计算器在线计算



球 圆球 体体积 表面积 周长 质量在线计算器 三贝计算网 23bei Com



薄球壳和球体转动惯量公式如何用推导而出 雨露学习互助



球的体积的公式推导 三人行教育网 Www 3rxing Org



椭圆体 椭球体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com


常用体积计算公式 电子工程世界 Eeworld



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ


球体体积公式是球体体积公式是什么



球台球带体积 侧面积 表面积计算公式与在线计算器 三贝计算网 23bei Com



用感覺理解球體表面積公式 Youtube



椭球中椭圆的面积公式 三人行教育网 Www 3rxing Org



忘記數學公式 Google工程計算機自動換算幾何圖形面積體積


Led屏各种面积 计算办法汇总点击查看 临沂led Led显示屏 临沂全彩显示屏 枣庄led 泰安led 日照led大屏幕 航空箱 航空箱厂家 航空箱生产厂家 山东鹰视电子科技有限公司



圆柱体积怎么算立方



U9762 U7a4d U548c U9ad4 U7a4d U516c U5f0f U5217 U68 Pdf U9762 U7a4d U548c U9ad4 U7a4d U516c U5f0f U5217 U68 1 U4ee5 U4e0b U70ba U5404 U5e38 U8b U5e73 U9762 U5716 U5f62 U7684 U5468 U754c U53ca U9762 U7a4d U4e4b U516c U5f0f U3002 A U4e09 Ud2
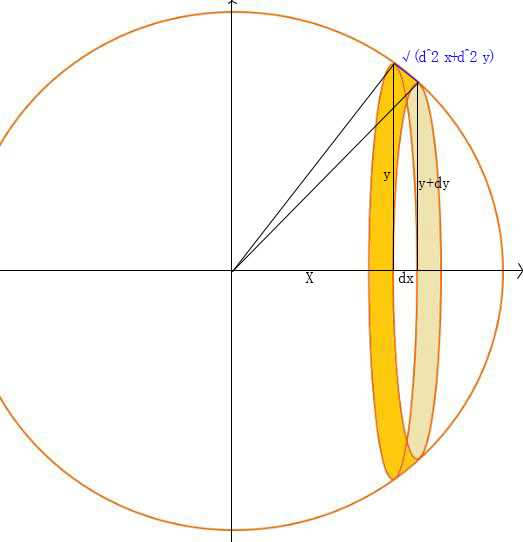


用积分推导球的表面积有哪些方法 知乎



Hkdse 數學練習平台 立方體其實都係prism 所以體積公式都係v Bh Facebook



球体体积积分球体积公式的推导 详细 最好是用积分推的



球面面积公式 你搜我答



对新编高中数学教材中球面积 球体积公式处理方案的考虑



球体体积计算公式 球体的体积 球体的体积公式 球体体积计算
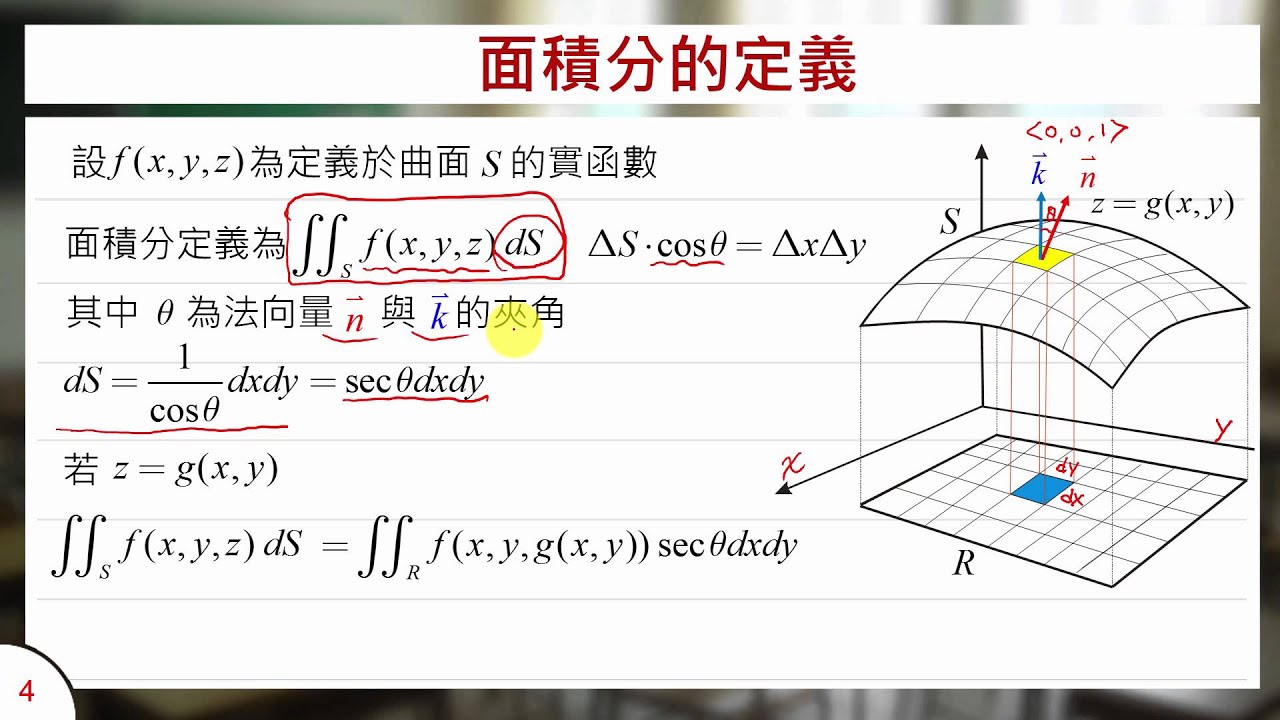


面積分 Youtube



三角柱体积公式 第1页 一起扣扣网


圓面積公式 圓形面積 來源故事 扇形 公式推導 圓面積公式 圓周長公式 中文百科全書


球的体积公式推导 孤云出岫 去留一无所系 朗镜悬空 静躁两不相干 Csdn博客 球的体积公式推导过程



球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和球面所圍 華人百科


球體體積鄧美愉11年6月 Ppt Download


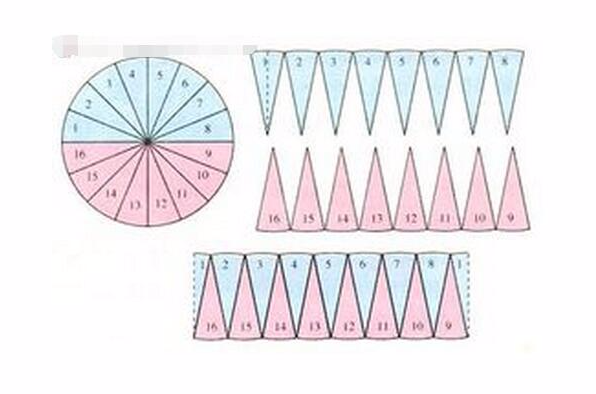
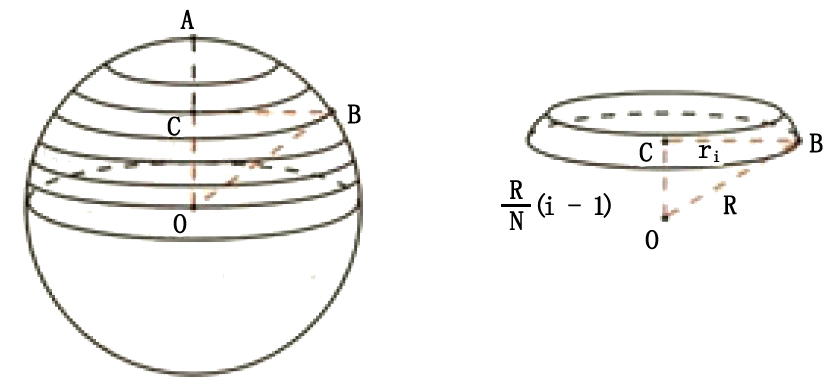
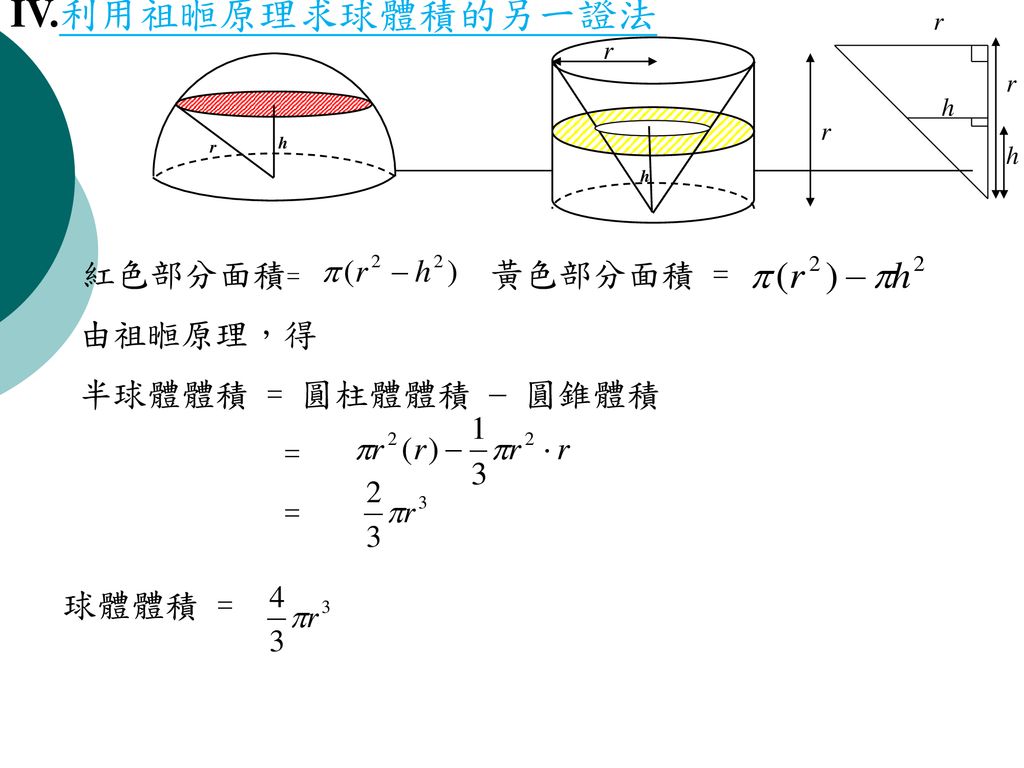
祖暅原理和球体面积体积公式推导 基础数学



橢球 一種二次曲面 是橢圓在三維空間的推廣 橢球在xyz 笛卡兒坐標系中的方程是 X 華人百科


球体体积公式推导图解 搜狗图片搜索


球的體積


写给5年级的学生 球公式是如何推导出来的 表面积



球体面积公式推导图解 第1页 一起扣扣网



球面积体积公式 球的面积体积 球的体积 圆球的面积



球冠 球缺的体积 面积 弧长 弦长在线计算器 三贝计算网 23bei Com



常见几何体面积及体积公式 Word文档在线阅读与下载 无忧文档


空間平面與等面積投影



高中立体几何 巧求空间几何体的体积的三个方法 雪花新闻


